Apresentação

Propriedades¶

As estruturas de grafos tem duas propriedades importantes:

Incidência: é a propriedade de uma aresta estar conectada a um vértice.
Adjacência: é a propriedade de dois vértices estarem conectados por intermédio de uma aresta. Dois vértices adjacentes também podem ser chamados de vizinhos.

Grafos Direcionados¶

Os grafos direcionados, conhecidos também como dirigidos, orientados ou digrafos, são grafos que possuem arestas com direção definida. Ou seja, as arestas apresentam um sentido que vai do vértice de origem até o vértice de destino.

Note

Definição formal: Um grafo dirigido G = (V,E) é definido por um conjunto não vazio V de vértices e um conjunto E de arestas, em que cada aresta e ∈ E é definida por um par ordenado de vértices (u, v), sendo ambos u e v ∈ V . O vértice u é o vértice origem, e v é o vértice destino da aresta e.

Exemplo de grafo direcionado — Fonte: Gomes, 2022

É possível visualizar na imagem que as arestas são representada por flechas que mostram a sua direção. Neste grafo os conjuntos de vértices e arestas são: V = {v1, v2, v3, v4} e E = {(v2, v1),(v4, v1),(v1, v3), (v2, v3),(v3, v4),(v4, v3)}. Note que agora, sendo um grafo dirigido, e1 = (v2, v1) ≠ (v1, v2).

Grafos Não Direcionados¶

Os grafos que possuem arestas que não indicam sentido são conhecidos como grafos não direcionados.

Info

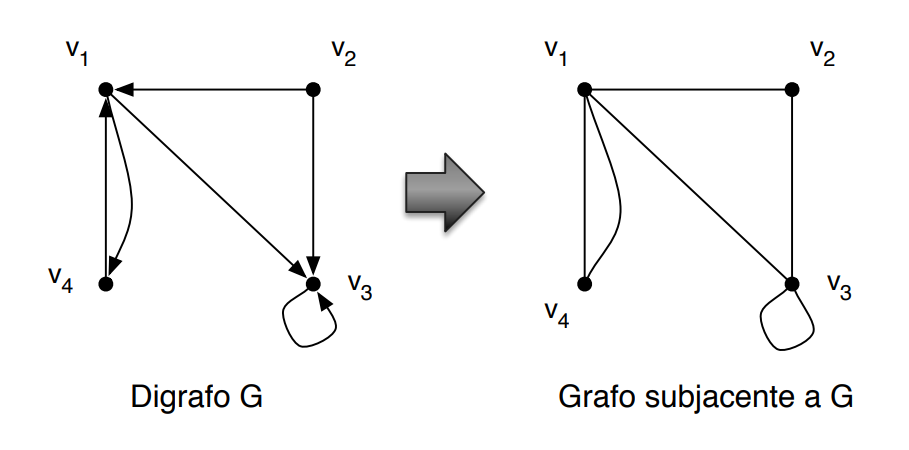
A partir de um grafo G direcionado é possível determinar seu grafo subjacente, que é um grafo não direcionado com as mesmas arestas do do grafo G. A imagem abaixo mostra essa relação.

Grafo subjacente a um grafo direcionado — Fonte: Gomes, 2022

O que é um grafo direcionado acíclico¶

Um grafo direcionado acíclico, também conhecido como DAG (Directed Acyclic Graph), é um grafo que não possui ciclos direcionados, ou seja, não existe um caminho que comece e termine no mesmo vértice seguindo a direção das arestas. Esse tipo de grafo é amplamente utilizado em contextos onde há dependências entre elementos, como na modelagem de fluxos de trabalho, representação de pré-requisitos em cursos, ordenação de tarefas em projetos, sistemas de compilação e estruturas de herança em programação orientada a objetos. Além disso, DAGs permitem a aplicação de algoritmos de ordenação topológica, fundamentais para organizar elementos de acordo com suas dependências.

Aplicações¶

Aplicações de tais grafos incluem:

Pré-requisitos entre disciplinas de um programa de graduação.
Herança entre classes de um programa orientado a objetos.
Restrições de agendamento entre as tarefas de um projeto.

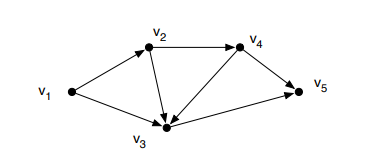
Exemplo de grafo direcionado acíclico — Fonte: Gomes, 2022

A imagem mostra um exemplo de grafo acíclico dirigido. Observa-se que, ao percorrer o grafo a partir de um vértice arbitrário v, não é possível retornar a esse mesmo vértice seguindo a direção das arestas.

O Que São Grafos Ponderados¶

Grafos ponderados são grafos cujas arestas possuem pesos que representam custos, distâncias ou outras métricas associadas. Cada aresta de um grafo ponderado possui um valor numérico chamado peso. Esses pesos podem representar distâncias, tempos, custos ou tarifas, dependendo do contexto. Por exemplo, em um sistema de companhias aéreas, as cidades podem ser representadas por vértices e os voos por arestas. Atribuindo diferentes tipos de pesos (distância, tempo de voo ou tarifa), é possível modelar problemas como encontrar o caminho mais curto ou o voo mais barato entre duas cidades.

Saber mais

Grafos ponderados também são amplamente utilizados para representar redes de computadores, onde os pesos podem indicar custos de comunicação, tempo de resposta ou distância física. Esses modelos ajudam a responder questões como qual é o caminho mais rápido ou mais barato entre dois pontos da rede.

Outro problema clássico envolvendo grafos ponderados é o Problema do Caixeiro Viajante (TSP), que busca o circuito de menor custo que visita todos os vértices de um grafo completo exatamente uma vez.

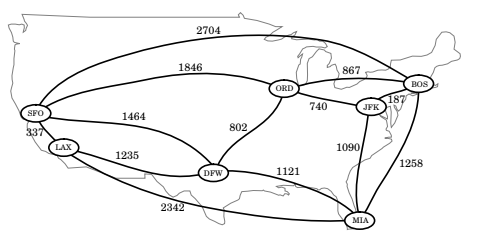
Exemplo de grafo ponderado — Fonte: Goodrich, 2013

A imagem mostra um grafo ponderado cujos vértices representam os principais aeroportos dos Estados Unidos e cujos pesos das arestas representam distâncias em milhas. Esse grafo possui um caminho de JFK até LAX com peso total de 2.777 (passando por ORD e DFW). Esse é o caminho de peso mínimo no grafo de JFK até LAX.

Algoritmo de Dijkstra¶

No contexto de grafos ponderados, o algoritmo de Dijkstra é um dos mais famosos e amplamente utilizados para resolver o problema do caminho de menor custo a partir de um único vértice de origem. Baseado no método guloso, ele constrói progressivamente uma "nuvem" de vértices alcançáveis, escolhendo em cada etapa o vértice mais próximo (com menor peso acumulado) ainda não processado. Essa abordagem permite encontrar o menor caminho, considerando os pesos das arestas, entre o vértice de origem e todos os demais vértices acessíveis no grafo. É utilizado em diversas aplicações práticas, como sistemas de navegação GPS, redes de computadores, logística, e análise de redes.

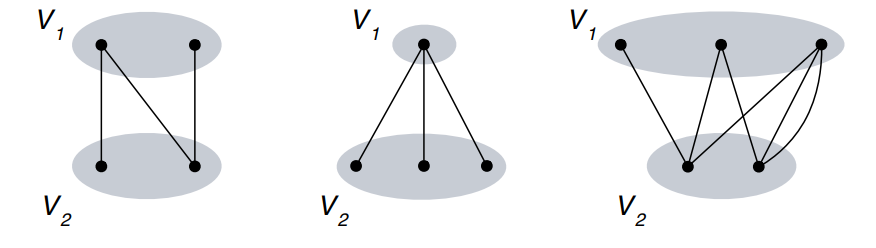
Grafos Bipartidos¶

Um grafo bipartido é aquele cujos vértices podem ser divididos em dois conjuntos disjuntos, U e V, de forma que nenhuma aresta liga vértices dentro do mesmo conjunto. A definição formal de um grafo bipartido é: um grafo bipartido G = (V₁ ∪ V₂, E) é definido por dois conjuntos disjuntos de vértices V₁ e V₂, tais que V₁ ∩ V₂ = ∅, e por um conjunto E de arestas, de modo que, para cada aresta e ∈ E, tem-se e = (u, v), com u ∈ V₁ e v ∈ V₂. Os conjuntos V₁ e V₂ são chamados de subconjuntos de bipartição de G.

Grafos Bipartidos Completos¶

Um grafo bipartido completo é um grafo bipartido no qual todo vértice do conjunto A é adjacente a todo vértice do conjunto B, ou seja, todas as possíveis arestas entre os vértices de A e B estão presentes. Esse grafo é denotado por Km,n, onde m=∣A∣e n=∣B∣, representando respectivamente o número de vértices em cada conjunto. Grafos bipartidos completos são amplamente utilizados em problemas de casamento, redes de fluxo e modelagem de relações entre dois grupos distintos.

Sobre as Representações¶

Representações dos grafos trata de como os grafos são representados no computador. Em implementações computacionais, grafos são modelados por três estruturas fundamentais: vértices, arestas e o próprio grafo (ou dígrafo, conforme o projeto). Os vértices representam os elementos básicos e geralmente incluem informações adicionais, como identificadores ou dados do problema. As arestas também podem carregar informações associadas, como número de voo, distância ou custo, refletindo características específicas do contexto modelado.

Lista de Arestas¶

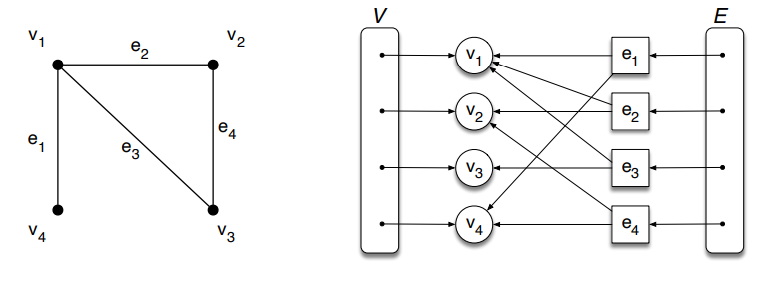
Lista de arestas é uma estrutura de dados, cuja principal característica é manter uma não ordenada de arestas. A operação de localização de uma aresta em particular e a localização de todas as arestas incidentes em um vértice não são eficientes.

A imagem representa a estrutura de grafos na memória, com duas coleções não ordenadas: uma para vértices (V) e outra para arestas (E), ambas contendo referências para os respectivos objetos. As referências estão representadas como setas na imagem. As arestas possuem ponteiros para os vértices aos quais estão conectadas, permitindo operações como verticesA(e) e oposto(v, e) em tempo constante. No entanto, os vértices não armazenam referências às arestas incidentes.

Operações mais comuns em estruturas de dados de grafos¶

Operação	Descrição
`getOrdem()`	retorna quantidade de vértices
`getTamanho()`	retorna quantidade de arestas
`vertices()`	retorna uma iteração de todos os vértices do grafo
`arestas()`	retorna uma iteração de todas as arestas do grafo
`insereV()`	instancia um novo vértice e o adiciona ao grafo
`removeV(v)`	remove o vértice `v` e todas as suas arestas incidentes
`insereA(u, v)`	instancia uma nova aresta incidente aos vértices `u` e `v`, e a adiciona ao grafo
`removeA(e)`	remove a aresta `e`
`adj(u)`	retorna uma iteração com todos os vértices adjacentes ao vértice `u`
`getA(u, v)`	retorna uma referência para a aresta de `u` para `v` ou `null` se os vértices não forem adjacentes. Para grafos não dirigidos, `getA(u, v)` e `getA(v, u)` produzem o mesmo resultado
`grauE(v)`	retorna o grau de entrada do vértice `v` em grafos dirigidos
`grauS(v)`	retorna o grau de saída do vértice `v` em grafos dirigidos
`grau(v)`	retorna o grau do vértice `v` em grafos não dirigidos. Alternativamente, pode‑se usar `grauE(v)` e `grauS(v)` para obter o mesmo resultado em grafos não dirigidos
`verticesA(e)`	retorna o par de vértices conectados à aresta `e`. Se o grafo for dirigido, o primeiro é a origem e o segundo é o destino da aresta
`oposto(v, e)`	para um vértice `v` incidente à aresta `e`, retorna o outro vértice incidente à mesma aresta
`arestasE(v)`	retorna uma iteração de todas as arestas de entrada do vértice `v`
`arestasS(v)`	retorna uma iteração de todas as arestas de saída do vértice `v`

Fonte: Gomes, 2022

Saber mais sobre o desempenho das operações

A estrutura de lista de arestas consome espaço O(m+n), onde n é o número de vértices e m o número de arestas, pois cada elemento ocupa espaço constante. As operações vertices() e arestas() têm desempenho O(n) e O(m), respectivamente. A principal limitação da estrutura é a ausência de referências das arestas nos vértices, o que torna operações como getA(u,v), grau(v), grauE(v), grauS(v), arestasE(v) e arestasS(v) de custo O(m). A adição de vértices e arestas é eficiente, com custo O(1), enquanto as remoções de arestas e vértices são O(m), devido à necessidade de percorrer a lista de arestas.

Listas de Adjacência¶

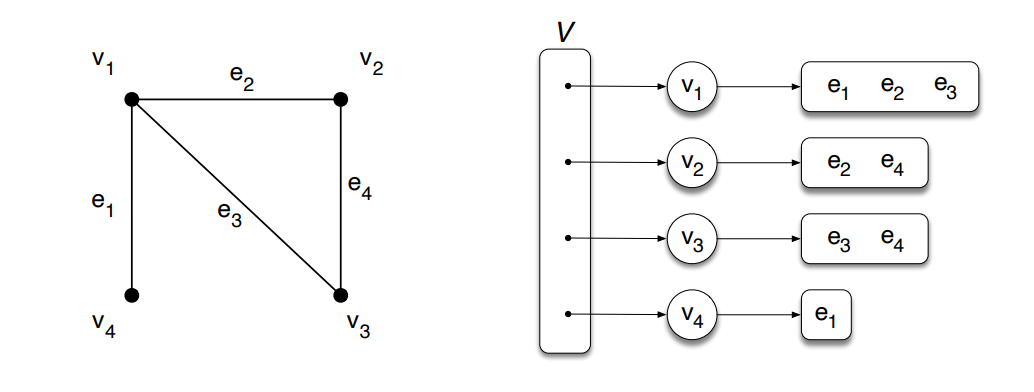
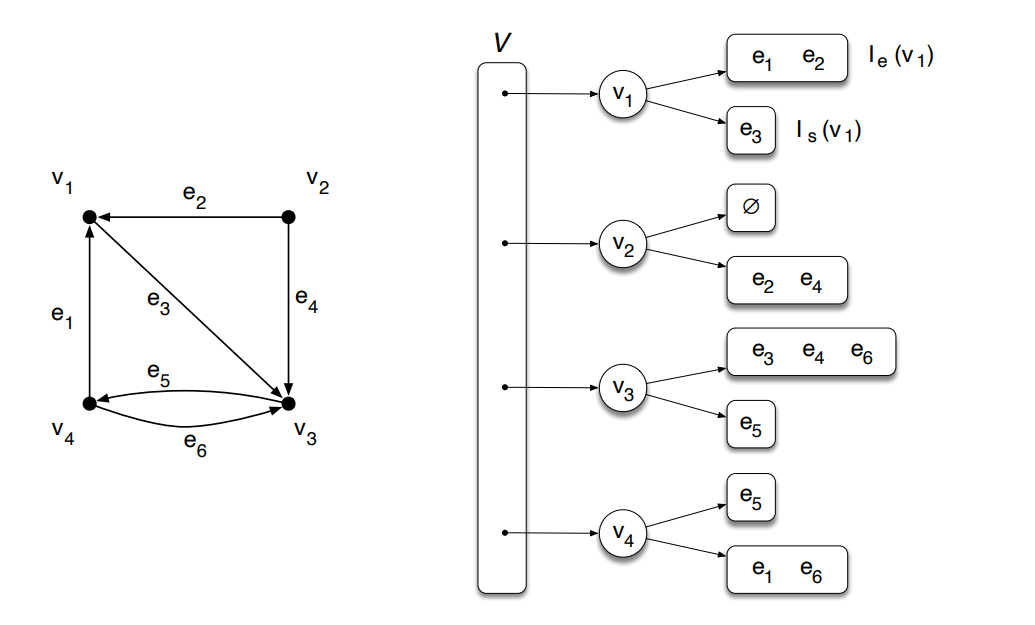
A estrutura de uma lista de adjacência de um grafo G = (V, E) consiste em uma coleção não ordenada iterável V de vértices e cada vértice mantém uma lista não ordenada de todas as suas arestas incidentes. Nessa estrutura, um vértice v possui a lista de incidência I(v), o que traz mais eficiência na determinação das arestas incidentes a um vértice. As listas de incidência são compostas por referências as arestas incidentes ao vértice. As listas que armazenam as arestas associadas a cada vértice são flexíveis (dinâmicas) e costumam ser implementadas com listas duplamente encadeadas, o que permite modificar a estrutura do grafo (como adicionar ou remover arestas) de forma mais eficiente. Quando se trata de grafos direcionados, cada vértice possui listas separadas para as suas arestas de entrada Ie(v) e saída Is(v).

O acesso aos elementos da estrutura do grafo depende da implementação da coleção de vértices V. Quando não há inserção ou remoção de vértices após a criação do grafo, V pode ser implementada como um array, e os vértices recebem identificadores numéricos correspondentes às posições nesse array. Nesse caso, o acesso à lista de incidência de um vértice é feito em tempo constante, ou seja, O(1).

Por outro lado, em contextos dinâmicos, onde vértices podem ser inseridos ou removidos, é necessário utilizar uma estrutura dinâmica para V, como listas duplamente encadeadas.

Nessa situação, o acesso à lista de incidência de um vértice exige uma busca na lista, resultando em tempo O(n).

Lista de adjacência de um grafo simples — Fonte: Gomes, 2022

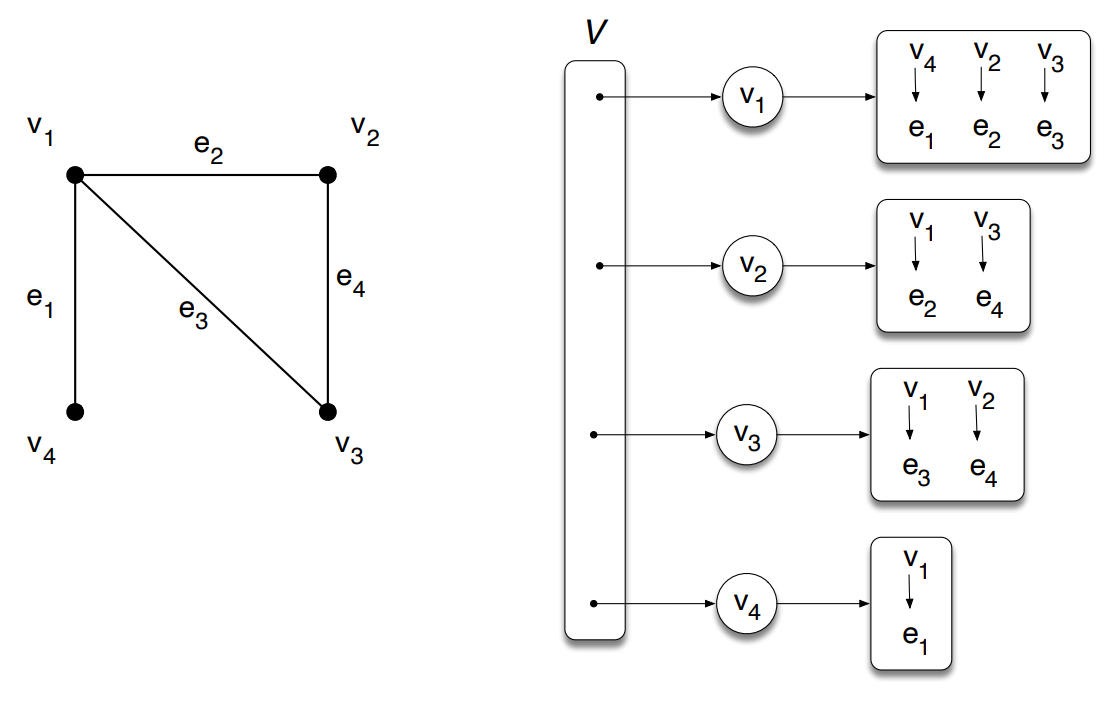
Explicação da imagem acima

A imagem acima representa esquematicamente a estrutura de listas de adjacência para um grafo não direcionado. À esquerda, observa-se um grafo composto por quatro vértices (v1, v2, v3 e v4) e quatro arestas (e1, e2, e3 e e4). As conexões entre os vértices são estabelecidas da seguinte forma: a aresta e1 liga v1 a v4; e2 liga v1 a v2; e3 liga v1 a v3; e4 liga v2 a v3. Como o grafo não é direcionado, todas as conexões são bidirecionais. À direita, tem-se a estrutura de dados correspondente, que representa o grafo por meio de listas de adjacência. A coleção V armazena os vértices, e cada vértice aponta para uma lista contendo as arestas incidentes a ele: v1 está associado às arestas e1, e2 e e3; v2 às arestas e2 e e4; v3 às arestas e3 e e4; e v4 à aresta e1. Assumimos que cada aresta representada no diagrama é uma instância única de um objeto aresta e que todas as arestas estão organizadas em uma coleção não ordenada e iterável, chamada de E. Isso permite que a estrutura seja percorrida com flexibilidade, e operações como o cálculo do grau de um vértice, identificação de vizinhos ou execução de algoritmos de busca possam ser feitas de forma eficiente

Explicação da imagem acima

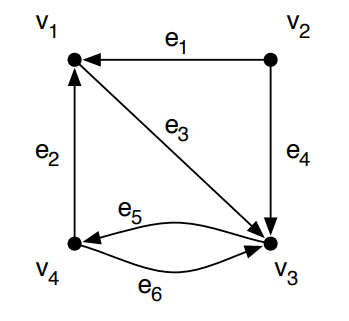
A imagem acima ilustra esquematicamente um grafo direcionado com vértices v1, v2, v3 e v4 e arestas e1, e2, e3, e4, e5 e e6, todas com direção indicada pelas setas. Nesse tipo de grafo, cada vértice mantém duas listas de incidência: uma contendo as arestas de entrada (ou seja, as que chegam ao vértice) e outra com as arestas de saída (aquelas que partem do vértice). Na estrutura representada à direita da figura, vemos que o vértice v1 possui as arestas e1 e e2 como entrada, e a aresta e3 como saída. O vértice v2 não possui arestas de entrada e tem e2 e e4 como arestas de saída. O vértice v3 possui e3, e4 e e6 como entrada, e apenas e5 como saída. Já o vértice v4 recebe a aresta e5 e possui como saídas as arestas e1 e e6. Essa forma de representação, com listas separadas para entrada e saída, é especialmente útil em algoritmos para grafos direcionados, como os de detecção de ciclos, ordenação topológica ou análise de fluxo, pois permite identificar rapidamente as relações de dependência e direção entre os vértices.

Mapas de Adjacência¶

A estrutura de mapas de adjacência é uma variação das listas de adjacência em que, para cada vértice, utiliza-se um mapa (ou dicionário) associando os vértices vizinhos às arestas correspondentes. Essa abordagem permite acesso eficiente à aresta entre dois vértices com complexidade O(1), desde que os mapas sejam implementados como hash maps. A estrutura mantém o uso de memória proporcional a O(m + n), onde m é o número de arestas e n é o número de vértices.

Mapa de adjacência de um grafo não direcionado — Fonte: Gomes, 2022

Explicação da imagem acima

A imagem acima mostra um grafo simples não direcionado à esquerda, com quatro vértices (v1, v2, v3 e v4) conectados por quatro arestas (e1, e2, e3 e e4), e sua correspondente representação por mapas de adjacência à direita. Nessa estrutura, cada vértice mantém um mapa no qual as chaves são os vértices vizinhos e os valores arestas que os conectam. Por exemplo, o vértice v1 está conectado aos vértices v4, v2 e v3 pelas arestas e1, e2 e e3, respectivamente. Esse tipo de organização permite acesso eficiente a qualquer aresta entre dois vértices específicos e evidencia a estrutura de conexões do grafo de forma clara e acessível para operações como busca ou verificação de adjacência.

O Que é a Varredura de Grafos¶

A varredura em grafos refere-se a uma classe de algoritmos que percorrem os vértices e arestas de um grafo de forma sistemática, visitando todos os seus elementos conectados. Esse processo é fundamental para entender a estrutura do grafo e resolver diversos problemas, como busca de caminhos, detecção de ciclos, componentes conexas, ordenação topológica, entre outros.

Métodos de Varredura¶

Existem dois métodos clássicos para varredura de grafos:

Busca em Largura (BFS - Breadth-First Search): Explora os vértices em níveis, visitando todos os vizinhos imediatos de um vértice antes de avançar para os vizinhos dos vizinhos. Utiliza uma fila para gerenciar os vértices a visitar.
Busca em Profundidade (DFS - Depth-First Search): Explora o grafo aprofundando-se o máximo possível em cada caminho antes de retroceder. Utiliza a recursão ou uma pilha para gerenciar o processo.

Nota

A escolha entre BFS e DFS depende do problema a ser resolvido. Por exemplo, BFS é útil para encontrar o caminho mais curto em grafos não ponderados, enquanto DFS é usado para detectar ciclos, componentes fortemente conectados, e ordenar vértices. Esses algoritmos são baseados em uma estrutura fundamental: um vetor ou conjunto que marca quais vértices foram visitados para evitar revisitas e loops infinitos.

Busca em Largura¶

A busca em largura (BFS - Breadth-First Search) é um algoritmo de varredura que explora um grafo a partir de um vértice inicial, visitando primeiro os vértices mais próximos (menor número de arestas) e depois os mais distantes. Funciona como uma “onda” que se espalha: primeiro visita todos os vizinhos imediatos do vértice inicial, depois os vizinhos desses vizinhos, e assim por diante.

Sobre a busca

Garante encontrar os caminhos mais curtos (em número de arestas) a partir do vértice inicial.
Forma uma árvore de busca, com o vértice inicial como raiz, e os demais vértices conectados por seus pais na busca.
Utiliza uma fila (queue) para gerenciar a ordem dos vértices a visitar.

Exemplo de Busca em Largura¶

Exemplo de aplicação em Python:

from collections import deque

def bfs(grafo, inicio):
    visitado = {v: False for v in grafo}
    distancia = {v: float('inf') for v in grafo}
    pai = {v: None for v in grafo}

    fila = deque()
    visitado[inicio] = True
    distancia[inicio] = 0
    fila.append(inicio)

    while fila:
        v = fila.popleft()
        print(f"Visitando: {v}")
        for vizinho in grafo[v]:
            if not visitado[vizinho]:
                visitado[vizinho] = True
                distancia[vizinho] = distancia[v] + 1
                pai[vizinho] = v
                fila.append(vizinho)

    return distancia, pai

# Exemplo de grafo
grafo = {
    0: [1, 2],
    1: [0, 3],
    2: [0, 4],
    3: [1],
    4: [2, 5],
    5: [4]
}

# Executa BFS a partir do vértice 0
distancias, pais = bfs(grafo, 0)

print("\nDistâncias a partir do vértice 0:")
for v in sorted(distancias):
    print(f"Vértice {v}: distância {distancias[v]}")

print("\nPais na árvore de busca:")
for v in sorted(pais):
    print(f"Vértice {v}: pai {pais[v]}")

Busca em Profundidade¶

A busca em profundidade (DFS) explora um grafo recursivamente: ao visitar um vértice, tenta seguir por um dos seus vizinhos ainda não visitado, aprofundando-se ao máximo. Quando não há mais vizinhos a explorar, o algoritmo retrocede (backtracking) para explorar outros caminhos possíveis.

Exemplos de Busca em Profundidade¶

DFS com vértice de origem único:

# Estados possíveis
NAO_VISITADO = 0
VISITADO = 1
ENCERRADO = 2

# Inicialização das estruturas
tempo = 0
estado = {}
fl = {}
ta = {}
te = {}

def visita_vertice(grafo, vi):
    global tempo
    estado[vi] = VISITADO
    tempo += 1
    ta[vi] = tempo

    for vj in grafo[vi]:
        if estado[vj] == NAO_VISITADO:
            fl[vj] = vi
            visita_vertice(grafo, vj)

    estado[vi] = ENCERRADO
    tempo += 1
    te[vi] = tempo

def busca_em_profundidade(grafo, r):
    global tempo, estado, fl, ta, te
    tempo = 0
    estado = {v: NAO_VISITADO for v in grafo}
    fl = {v: None for v in grafo}
    ta = {}
    te = {}

    visita_vertice(grafo, r)
    return estado, fl, ta, te

# Exemplo de grafo
grafo = {
    0: [1],
    1: [2],
    2: [0, 3],
    3: []
}

# Executa DFS a partir do vértice 0
estado, fl, ta, te = busca_em_profundidade(grafo, 0)

# Exibindo os resultados
print("Pais:", fl)
print("Tempo de descoberta:", ta)
print("Tempo de término:", te)

DFS com várias origens (para grafos não conexos ou dirigidos):

def busca_profundidade_todos(grafo):
    global tempo, estado, fl, ta, te
    tempo = 0
    estado = {v: NAO_VISITADO for v in grafo}
    fl = {v: None for v in grafo}
    ta = {}
    te = {}

    for v in grafo:
        if estado[v] == NAO_VISITADO:
            visita_vertice(grafo, v)

    return estado, fl, ta, te

# Outro exemplo com vértices desconectados
grafo = {
    0: [1],
    1: [],
    2: [3],
    3: []
}

estado, fl, ta, te = busca_profundidade_todos(grafo)

print("Pais:", fl)
print("Tempo de descoberta:", ta)
print("Tempo de término:", te)

Algoritmo de Kruskal (Árvore Geradora Mínima)¶

Kruskal é um algoritmo guloso que encontra a árvore geradora mínima (MST) em grafos ponderados e conexos. Ele ordena as arestas por peso e vai adicionando as menores que não formam ciclos, utilizando a estrutura de união-encontro para acompanhar os componentes conectados. É ideal para grafos esparsos e garante solução ótima. Aplicações incluem projetos de redes como cabos de fibra ou estradas entre cidades.

Algoritmo de Floyd-Warshall (Todos os Pares de Menor Caminho)¶

Calcula os caminhos mínimos entre todos os pares de vértices, inclusive com pesos negativos (sem ciclos negativos). Usa matriz de distâncias e programação dinâmica, com complexidade O(n³), ideal para grafos pequenos ou médios. É versátil e útil para problemas como roteamento de redes, logística e construção de matrizes de distância. Simples de implementar, resolve “tudo de uma vez”.

Coloração de Grafos (Mínima Coloração)¶

Consiste em colorir os vértices de um grafo para que vértices adjacentes não compartilhem a mesma cor, buscando o menor número possível de cores. Determinar a coloração mínima é um problema NP-completo. Aplicações incluem alocação de horários, uso de registradores em compiladores e coloração de mapas. Métodos práticos incluem heurísticas, backtracking e algoritmos gulosos.