Introdução
Primeiro Registro¶
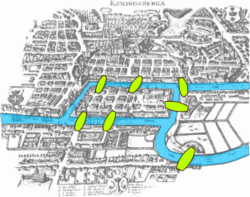
O primeiro registro histórico do uso de grafos foi em 1736 com a publicação de Leonhard Euler “Solutio problematis ad geometriam situs pertinentis” (“A solução de um problema relacionado à geometria de posição”), em que ele discutia o problema das sete pontes de Königsberg.
Fonte: Paoletti, 2006
O Problema¶
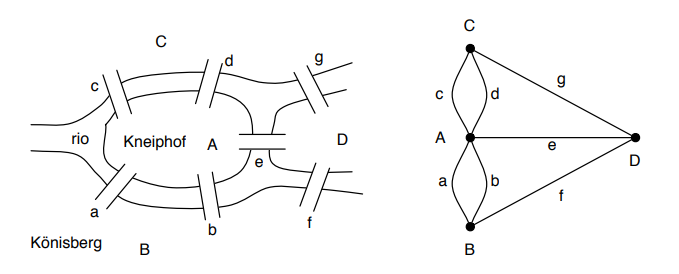
As quatro partes da cidades (A, B, C, D) eram conectadas por sete pontes (a, b, c, d, e, f, g) e o problema das sete pontes consistia em se era possível sair de qualquer ponto da cidade, atravessar as sete pontes somente uma vez e retornar ao ponto de partida.
Fonte: Gomes, 2022
No seu trabalho em 1730, Euler provou através de grafos que era impossível, para isso ele representou as partes da cidade como pontos (vértices) e as pontes como arestas conectando esses pontos. Esse diagrama é considerado o primeiro registro histórico de grafos.
Definição¶
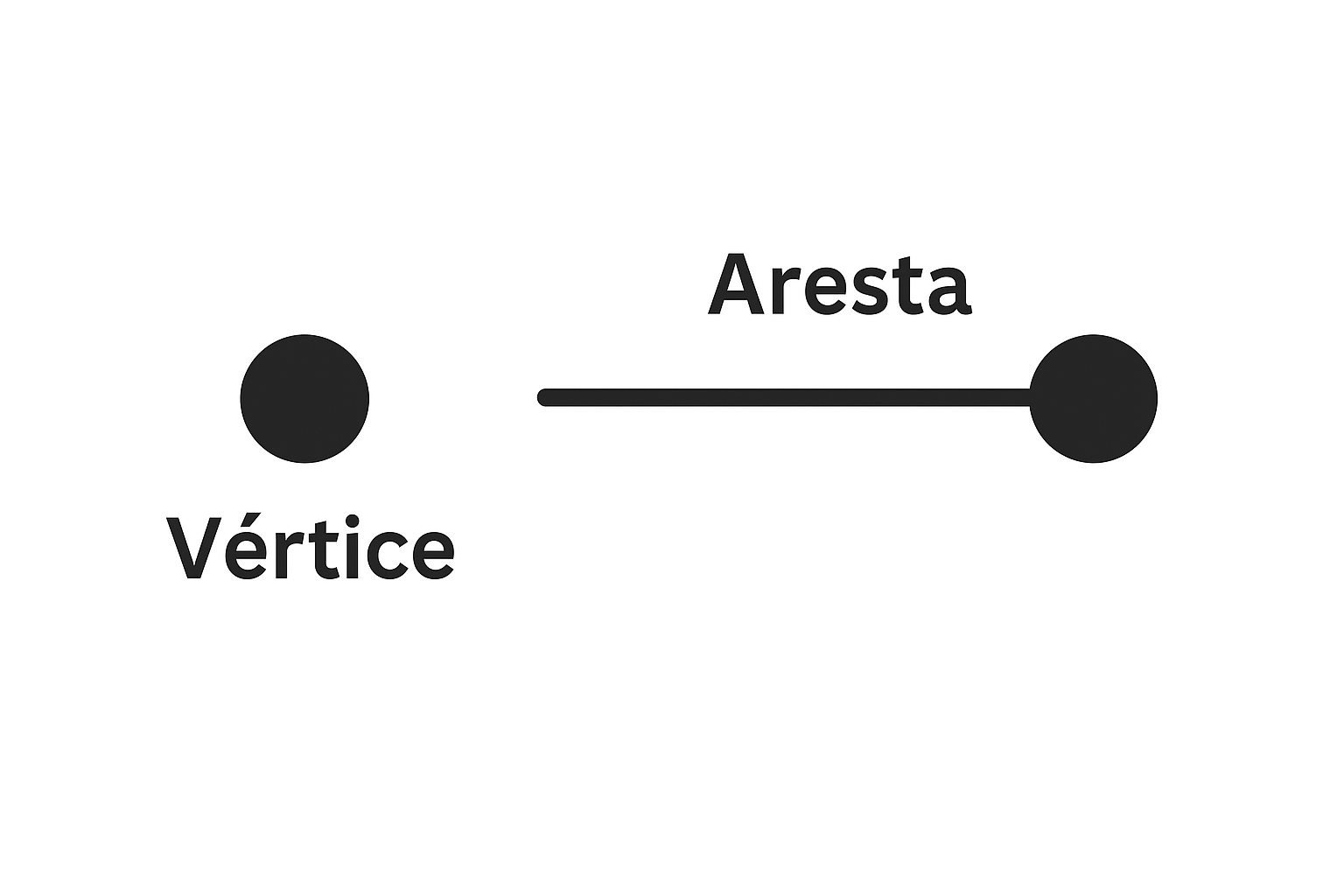
Um grafo é uma estrutura matemática utilizada para representar relações entre objetos. Nessa representação, os objetos são chamados de vértices e as conexões entre eles são denominadas arestas (ou arcos, no caso de grafos direcionados). Visualmente, grafos são compostos por pontos (vértices) conectados por linhas (arestas).
Os grafos têm ampla aplicação em diversas áreas, como mapeamento geográfico, definição de rotas, redes de computadores, engenharia elétrica, entre outras. Sua versatilidade permite modelar diferentes tipos de problemas, como circuitos eletrônicos, caminhos em mapas e até relações entre registros em bancos de dados.
Note
Definição formal de grafo: Um grafo G = (V,E) é definido por um conjunto não vazio V de vértices e um conjunto E de arestas, em que cada aresta e ∈ E é definida por um par não-ordenado de vértices (u, v), sendo ambos u e v ∈ V .
Fonte: Wikipédia (adaptado)
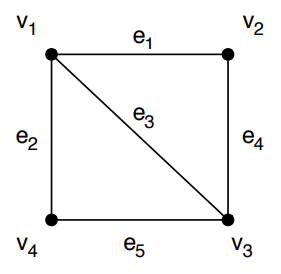
Fonte: Gomes, 2022
Nesse exemplo teríamos os seguintes conjuntos: V = {v1, v2, v3, v4} e E = {(v1, v2),(v1, v4),(v1, v3),(v2, v3),(v4, v3)}.